Create a Simple Search Engine with Python and Math

Have you ever imagined how Google search engine works? How can their system rank millions of documents and return very accurate results to every user every day? Do you know that we can create a simple text search engine using just math and some coding? That’s exactly the topic I’m going to cover in this article, and by the end of the post, you will be capable of implementing your own version of a search engine and understanding the concepts behind a Vector Space powered Search Engine.

Vector Space Model

Imagine that you are searching for information about airplanes and want the results to be ordered by relevance. All the information you have about airplanes is stored inside thousands of documents in a database. These documents are completely raw and unstructured; all you have is the text itself. You can’t search the term “airplane” on a category relation from your tables. So, how can the computer find which documents are relevant to you and order them? This can be done using the vector space algebraic model.

The algebraic vector space model can represent objects (text in our case) as vectors of identifiers, like index terms. This model operates in an n-dimensional plane, where each dimension corresponds to a unique term from our index. For example, if we have a text “airplane fly,” we would have two indexes: “airplane” and “fly.” These two indexes can be represented in a plane like this:

$Vector Representation$

Now, let’s get this very simple scenario for the explanation, with a simple one word query and two documents with no new words(new words would update our index and our plain, adding new dimensions to it):

query = 'airplane'
doc1 = 'airplane fly'
doc2 = 'fly'

Simple Scenario

Consider a simple scenario with a one-word query and two documents with no new words (new words would update our index and plane, adding new dimensions to it):

$Vector Scenario$

Now, let’s change our scenario to a more usable form:

If this image reminds you of something, congratulations, you have a good memory and recognize vectors representation. Our strings were converted into groups of numbers that represent coordinates on a plane. Let’s draw the resultant vectors:

$Resultant Vectors$

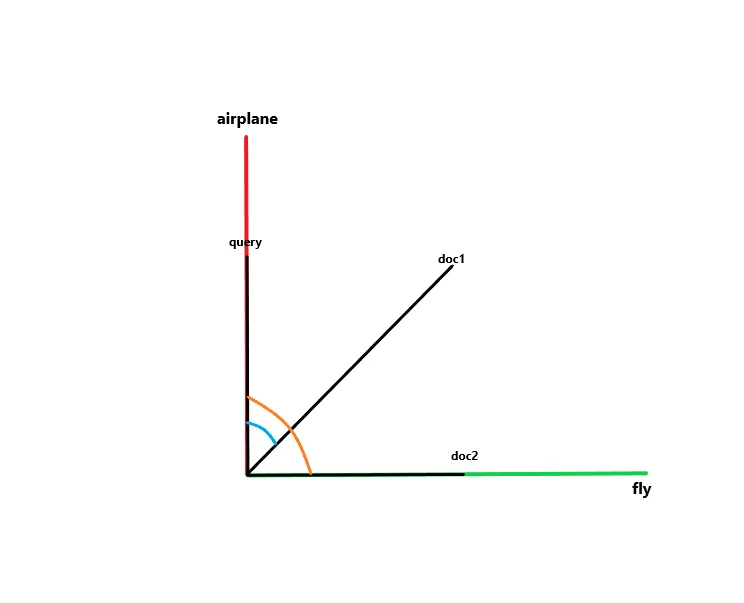
We have all our documents and our query plotted on the plane using both indexes “airplane” and “fly” as the X and Y axes. For humans, it’s easy to see that doc1 is the most relevant and should be returned as the result because it has a smaller angle with the query vector compared to doc2. This indicates that doc1 is more similar to the query than doc2. This entire process can be performed by calculating the cosine similarity between the documents and the query using the following formula:

\text{cosine similarity} = \frac{\text{Dot Product}}{\text{Magnitude of Query} \times \text{Magnitude of Document}}

Breaking Down the Formula

Dot Product

The dot product is defined as the sum of the products of the corresponding components of two vectors. For example, if we apply it to the query and doc1, the result would be 1.

Magnitude

Magnitude determines the size or length of a vector. It is calculated as:

\text{Vector} = \sqrt{x^2 + y^2}

For our example, the magnitude would be 1.414213562373095.

Final Result

Combining both parts:

\text{Cosine Similarity} = \frac{1}{1.414213562373095} \approx 0.7071067811865475

This result represents a 70.71% similarity between the query and the document, indicating a strong relevance.

Coding It

Now that we’ve covered the mathematical part, we can transform everything into code. The first step is to create the index terms and term frequencies from each text. We start by removing noise from the text (numbers, non-ASCII characters, punctuation, etc.) and then create a dictionary with index terms as keys and their frequencies as values.

from pylexitext.text import Text
from collections import Counter

def create_concordance(text):
  text = Text.noise_removal(text)
  return dict(Counter(text.split()))

If we execute this method on the texts, the result would be this:

print(f'query: {create_concordance('airplane')}')
print(f'doc 2: {create_concordance('airplane fly')}')
print(f'doc 3: {create_concordance('fly')}')
# query: {'airplane': 1}
# doc 2: {'airplane': 1, 'fly': 1}
# doc 3: {'fly': 1}

The next step would be convert the formula. As we know, we need two main calculations to find our result, the dot product and magnitude, both this methods are already implemented on numpy, but, I’m going to implement it anyway, so you can understand it better by seeing real code. Below, you can check both functions and the respective counterparts from numpy:

import math

# The equivalent to this method in numpy would be: numpy.linalg.norm
def magnitude(terms_frequency):
  total = 0
  for _, count in terms_frequency.items():
    total += count ** 2
  return math.sqrt(total)

# The equivalent to this method in numpy would be: numpy.inner
def dot_product(query_fq, doc_fq):
  res = 0
  for term, freq in query_fq.items():
    if term in doc_fq:
      res += freq * doc_fq[term]
  return res

Now, we just need to wrap it all together, to create a function that returns the cosine similarity between two text objects. Below you can check the final function to calculate the cosine similarity, this function already expects inputs as terms frequency dictionary(example at result_concordance.py gist):

def cos_similariry(query_fq, doc_fq):
  return dot_product(query_fq, doc_fq) / (magnitude(query_fq) * magnitude(doc_fq))

If we executed it with the same input we used to perform the formulas above, the result would be exactly 0.7071067811865475 as expected. Of course this piece of code was made to just compare two objects, a real use case would need to iterate over all the documents. Below you will find an example how it would looks like(with a simple modification to avoid divisions by 0):

def search(query, documents, top_results=10):
  res = []
  query_fq = create_concordance(query)

  for doc in documents:
    doc_fq = create_concordance(doc)
    magnitude_result = magnitude(query_fq) * magnitude(doc_fq)

    if magnitude_result != 0:
      dot_p = dot_product(query_fq, doc_fq)
      res.append(((dot_p / magnitude_result), doc))

  res.sort(reverse=True)
  return res[:top_results]

This method would process multiple documents and return the top ten results, ordered by relevance.

Conclusion

In a world where we always need better ways to discover and find relevant data, search engines are a really important topic to master and study, with this simple solution, you can already process thousands of documents and find the top relevant results! I really recommend that real world implementations should be improved to include some performance related changes, like filters and edge cases !

If you want to use a ready solution for a search engine with a more robust implementation or just want to see how it looks like, I really recommend that you check pylexitext, a python library I have created and have been working on, there you can find a collection of text related engines and NLP stuff, created to be more usable to anyone. Feel free to contribute if you want, it would be a pleasure work with you!

References & auxiliary material

https://boyter.org/2010/08/build-vector-space-search-engine-python/
https://www.youtube.com/watch?v=ainS3BBn7rs
https://en.wikipedia.org/wiki/Vector_space_model
https://en.wikipedia.org/wiki/Cosine_similarity
https://en.wikipedia.org/wiki/Magnitude_(mathematics)#Euclidean_vector_space
https://en.wikipedia.org/wiki/Dot_product
https://numpy.org/doc/stable/reference/generated/numpy.inner.html
https://numpy.org/doc/stable/reference/generated/numpy.linalg.norm.html
https://github.com/vicotrbb/Pylexitext